Simbolización de Expresiones Algebraicas
Como señalábamos en la anterior sección es posible escribir operaciones algebraicas
con una sintaxis muy semejante a la que estamos acostumbrados:
<Variable> ^ <Exponente>
Veamos este ejemplo:
Mathematica 3.0 for Linux
Copyright 1988-97 Wolfram Research, Inc.
-- Motif graphics initialized --In[1]:= x^3
Out[1]= x3
In[2l:= 2*y^7
Out[2]= 2y7
In[3]:= 3w^2
Out[3]= 3w2
In[4]:= -2x^2
Out[4]= -2x2
In [5]:= x^3+x^2-x-1
Out[5]= - 1 - x + x2 + x3
|
Como se puede apreciar es posible escribir cualquier letra que funcione como variable.
Además, el reconocimiento de la expresión por parte de Mathematica se logra al
reescribirla pero ahora la expresión comienza con el término de menor exponente hasta el
de mayor exponente.
Asignacion de Valores Numéricos a Variables
Podemos sustituir cualquier variable por un valor numérico o por una expresión
algebraica y de esta forma, lograríamos manejar más fácilmente expresiones largas tal
como se hace en la vida real.
<Variable>=<Valor numérico>
<Variable> = <expresión> |
Asignación. |
| <Variable>=. |
Elimina cualquier valor de la variable. |
Veamos un ejemplo:
Mathematica 3.0 for Linux
Copyright 1988-97 Wolfram Research, Inc.
-- Motif graphics initialized --In[1]:= q = 5
Out[1]= 5
In[2l:= w = 32
Out[2]= 32
In[3]:= q * w
Out[3]= 160
In[4]:= % - q
Out[4]= 155
In [5]:= w
Out[5]= 32
In [6]:= w=.
In [7]:= q=.
In [8]:= q * w
Out[8]= qw
|
Podemos distinguir con claridad la forma de asignar valores a variables y el manejo de
esas variables (como en la entrada 3), así como la posterior remoción de los valores de
dichas variables.
Evaluación de Una Expresión con Respecto a un Valor Numérico
Es posible evaluar una expresión dada con respecto a un valor numérico en la cual se
sustituye la variable por el valor definido. Esto se logra de la siguiente forma:
<Expresión> /. <Variable> -><Valor
numérico>
Como hemos visto, se utilizó un nuevo filtro (" /. ") para poder separar a
la expresión de la evaluación y se introdujo un nuevo elemento, (" -> "),
que funciona como apuntador y nos será muy necesario para cálculos posteriores.
Observemos este ejemplo:
Mathematica 3.0 for Linux
Copyright 1988-97 Wolfram Research, Inc.
-- Motif graphics initialized --In[1]:=
x^3+x^2-x-1
Out[1]= - 1 - x + x2 + x3
In[2l:= % /. x -> 3
Out[2]= 32
In[3]:= 15x^4+94x^3-5x^2-164x+60 /. x -> 15
Out[3]= 1073100
|
NOTA: Esta notación se utiliza para sustituir la variable por un valor numérico y
se puede confundir con la que se emplea en Cálculo para obtener límites.
Operaciones Fundamentales
El tratamiento de operaciones algebraicas (suma,resta,multiplicación, división) es
similar a la nomenclatura real; únicamente se tendrá que poner énfasis en el uso de
paréntesis para que Mathematica pueda distinguir las expresiones así como la operación
que se desee.
Observemos el siguiente ejemplo:
Mathematica 3.0 for Linux
Copyright 1988-97 Wolfram Research, Inc.
-- Motif graphics initialized --In[1]:=
(x^3+3x^2-8x-1)+(-x^3+2x^2-3x+5)
Out[1]= 4 - 11x + 5x2
In[2l:= (x+Sqrt[2])(x-Sqrt[2])(x+4)
Out[2]= (4 + x)(-Sqrt[2] + x)(Sqrt[2] + x)
In[3]:= %1 / (x -3)
Out[3]= 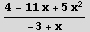
|
Nótese que en la segunda y tercera salida Mathematica no devuelve el resultado
esperado sino que realiza el proceso de reconocimiento por lo que será necesario indicar
al programa lo que queremos mediante comandos.
Manejo de Comandos Básicos
El tratamiento de las expresiones es una de las aplicaciones más poderosas del
Mathematica, ya que es capaz de factorizar, expander, ejecutar productos notables,
simplificar, ordenar bajo requerimientos concretos y particulares como agrupaciones por
denominador común,por grado de potencias, por letras, etc. dando todo esto un tópico
sumamente interesante a Mathematica.
Un acercamiento al uso de los comandos mencionados en la sección anterior se propone a
continuación (se utilizará la abreviatura "expr" para referirnos a la
expresión):
| Expand [<Expr> ] |
Efectúa los productos y cocientes ofreciendo el resultado en una sola expresión. |
| Factor [<Expr> ] |
Factoriza la expresión a su mas mínima expresión. |
| Simplify [<Expr> ] |
Descompone la expresión en fracciones simples. |
| ExpandAll [<Expr>] |
Expande todos los elementos posibles que se puedan obtener dado una operación. |
| Together [<Expr>] |
Acomoda todos los términos en un común denominador. |
| Apart [<Expr>] |
Separa todos los términos con denominador simple. |
| Cancel [<Expr>] |
Elimina los factores comunes en el denominador y numerador. |
| Collect [<Expr>] |
Reúne todas las potencias de la variable x. |
| FactorTerms [<Expr> , <Variable>] |
Pone como factor todo aquello que no depende de la variable nombrada en
"variable", en una expresión algebraica. |
Detengámonos en este ejemplo:
Mathematica 3.0 for Linux
Copyright 1988-97 Wolfram Research, Inc.
-- Motif graphics initialized --In[1]:=
e=(x-1)^2(x+2)/((x+1)(x-3)^2)
Out[1]= 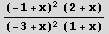
In[2]:= Expand[e]
Out[2]= 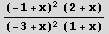
In[3]:= ExpandAll[e]
Out[3]= 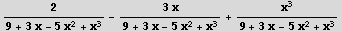
In[4]:= Together[%]
Out[4]= 
In[5]:= Apart[e]
Out[5]= 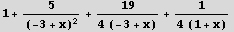
In[6]:= Factor[e]
Out[6]= 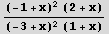 |
Manejo de Comandos Avanzados
| Expand [<Expr>, Trig->True ] |
Expande las funciones trigonométricas escribiéndola en su máxima expresión. |
| Factor [<Expr>, Trig->True ] |
Comando que realiza la operación inversa al anterior. |
| PowerExpand [<Expr> ] |
Distribuye el exponente en términos que operen con más de dos variables. |
| Coefficient [<Expr>, <Variable> ] |
Señala los coeficientes de la variable en cuestión. |
| Exponent [<Expr>, <Variable> ] |
Obtiene la potencia mayor de la variable contenida en una expresión. |
Es posible que en varias ocasiones escribamos un término erróneamente en una
expresión. El siguiente comando reemplaza dicho término:
ReplacePart [<Expr>,<Término>, n ]
Veamos en seguida un ejemplo de lo expuesto:
Mathematica 3.0 for Linux
Copyright 1988-97 Wolfram Research, Inc.
-- Motif graphics initialized --In[1]:=
(x+Sqrt[5])(x-Sqrt[5])(x+4)
Out[1]= 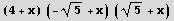
In[2]:= Expand[%]
Out[2]= - 20 - 5x + 4x2 + x3
In[3]:= Factor[%]
Out[3]= (4 + x) (- 5 + x2)
In[4]:= ExpandAll[%]
Out[4]= - 20 + 5x + 4x2 + x3
In[5]:= Part[%,2]
Out[5]= -5x
In[6]:= ReplacePart[%4,8x,2]
Out[6]= -20 + 8x + 4x2 + x3
In[7]:= Exponent[%6,x]
Out[7]= 3
In[8]:= Coefficient[%2,x]
Out[8]= -5
In[9]:= p=((x^3+8)(x^3-8))/((x^2-4)(x^2+2x+4))
Out[9]= 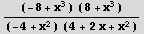
In[10]:= ExpandAll[%]
Out[10]= 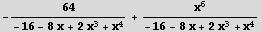 |
|